 | |
Łamigłówki logiczneSeweryn WęgielnikSpis treściZadanie 11. Skarpetki↥ Sprawdź rozwiązanieW szufladzie w ciemnym pokoju leżą 24 skarpetki czerwone i 24 skarpetki białe. Jaka jest najmniejsza ilość skarpet, które muszę wyciągnąć aby mieć pewność, że mam co najmniej dwie skarpety w tym samym kolorze? Zadanie 12. Włosy ↥Załóżmy, że Nowy Jork ma więcej mieszkańców, niż ma na głowie jego dowolny mieszkaniec, oraz że żaden mieszkaniec Nowego jorku nie jest zupełnie Łysy. Czy wynika stąd koniecznie, że co najmniej dwie osoby muszą mieć dokładnie taką samą liczbę włosów? Zadanie 13. Pcim ↥W Pcimiu
Jaka jest największa możliwa liczba mieszkańców Pcimia? Zadanie 14. 30 groszy↥Dwie monety dają w sumie 30 gr choć jedna z nich nie jest dziesięciogroszówką. Jak to jest możliwe?Zadanie 15. Przepisy prawa↥Czy przepisy prawa kanonicznego zezwalają mężczyźnie na poślubienie siostry wdowy po nim? Zadanie 16. Portret↥Pewien człowiek przyglądał się jakiemuś portretowi. Ktoś go spytał: "Czyjemu portretowi się przyglądasz?" Ăw człowiek odpowiedział: "Nie mam ani braci, ani sióstr, ale ojciec tego człowieka jest synem mojego ojca". Czyjemu portretowi przygląda się ten człowiek? Zadanie 17. Klasówka↥ Sprawdź rozwiązanieNauczyciel przyrzekł na przyszły tydzień klasówkę - "niespodziankę" tzn., że nikt nie będzie się jej spodziewał. Uczniowie rozumują tak: gdyby klasówka była w przyszły piątek to już w czwartek wiedzielibyśmy o niej skoro aż do tego dnia jej nie było. Klasówka w piątek nie może więc być, bo co to za niespodzianka, o której wszyscy wiedzą! Rozumując w ten sam sposób dochodzimy do wniosku, że i w czwartek nie może być. W takim razie klasówka "niespodzianka" nie może być w żaden dzień tygodnia. Czy, jeśli nauczyciel zrobił jednak klasówkę w piątek, to złamał przyrzeczenie? Zadanie 18. Pociągi↥Pociąg wyjeżdża z Olsztyna do Warszawy. W godzinę później drugi pociąg wyjeżdża z Warszawy do Olsztyna. Pierwszy pociąg zrobił jednogodzinny postój w Olsztynku. Który pociąg będzie bliżej Warszawy w momencie spotkania? Zadanie 19. Kłamcy↥W pewnym mieście są ludzie mówiący tylko prawdę - nazywają się rycerzami i ludzie natorycznie kłamiący - zwani łotrami. Spotykasz trzech ludzi A, B i C, pytasz A "Kim jesteś", A odpowiada ale niewyraźnie więc pytasz się B "Co powiedział A?", B odpowiada, "A powiedział, że jest łotrem" w tym momencie C powiedział "Nie wierz B on kłamie!". Kim są A i B? Raymond M. SmullyanRaymond Smullyan jest filozofem, znakomitym pianistą i zawodowym magikiem. Napisał wiele popularnych książek. Zadanie 21. Kłamcy↥Skazany na śmierć ma wygłosić zdanie. Jeśli będzie ono prawdziwe ma zostać utopiony; jeśli będzie fałszywe ma zostać powieszony. Jakie powinien wygłosić zdanie, żeby wprawić w zakłopotanie katów? Zadanie 22. Głupi obrońca↥ Sprawdź rozwiązaniePewnego człowieka sądzono za udział w rabunku. Oskarżyciel i obrońca wygłosili następujące zdania. Oskarżyciel: "Jeśli oskarżony jest winny, to ma on współwinnego." Obrońca: "To nieprawda!" Dlaczego była to najgorsza rzecz, jaką mógł powiedzieć obrońca? Zadanie 23. Roślina↥Gdyby pewna roślina urosła jeszcze o trzy stopy, byłaby dwa razy wyższa, niż gdyby zmalała o pół stopy. Jak wysoka jest roślina? Zadanie 24. Wielbłądy↥Hussan miał osiem wielbłądów, ale pewnego pechowego miesiąca zdechły wszystkie prócz pięciu. Ile wielbłądów zostało? Oczywiście, że trzy - odpowiedział król. - Każdy osioł mógłby to powiedzieć. Zgadzam się z ostatnią odpowiedzią króla. Czy Ty także? Zadanie 31. Wszechmogący Bóg↥Bóg jest wszechmogący. Tak głosi większość religii. Czy w takim razie może stworzyć taki kamień, którego nie podźwignie? Zadanie 32 Kamień wszystko powalający↥Niech kamień wszystko powalający nazywa się superkamień a drzewo odporne na wszystko superdrzewem. Czy superkamień złamie superdrzewo? Zadanie 33 Pytanie o drogę↥Wiadomo, że na pewnej wyspie są ludzie zawsze kłamiący (Kłamcy) i ludzie prawdomówni (Prawdomówni) doszłaś do rozwidlenia dróg i nie wiesz, którą drogę wybrać do wioski Prawdomównych. Na szczęście na rozstaju stoi wyspiarz. Możesz zadać tylko jedno pytanie żeby dowiedzieć się o właściwą drogę. Podaj takie pytanie. Zadanie 34 Kapelusze↥Mamy w kartonie pięć kapeluszy: trzy czarne i dwa białe. Ustawiamy trzech ludzi jeden za drugim tak, że mogą widzieć tylko poprzedników. Każdemu nakładamy kapelusz. Pytamy się ostatniego (tego który widzi dwóch poprzedników) jaki ma kapelusz. Odpowiada, że nie wie. Zapytany środkowy też nie wie jaki ma kapelusz ale pierwszy, który nie widzi żadnego kapelusza zapytany odpowiada, że wie. Jaki kapelusz ma pierwszy człowiek? Zadanie 35 Tata i jego dzieci↥
Po kilku latach niewidzenia spotyka się dwóch panów na przystanku autobusowym. Po wymianie zdawkowych pytań jeden z nich powiada, że ma dzieci.Dialog wyglądał mniej więcej tak: Zadanie 36 Niegrzeczne dzieci↥W pewnej szkole, w pewnej klasie odbyło się ostatnie przed wakacjami zebranie rodziców. Wychowawca zagaił tak: "Wiem, że niektóre z waszych dzieci palą papierosy. O szkodliwości tego nałogu nie będę się rozwodził. Teraz podejdę i każdemu rodzicowi wręczę karteczkę z napisaną ilością dzieci palących wyłączając własne dziecko tego rodzica, którego dziecko pali, tzn. rodzic, którego dziecko pali będzie miał na karteczce liczbę o jeden mniejszą od liczby na karteczce wręczonej rodzicowi grzecznego dziecka. Ĺťeby nie wzbudzać niezdrowych emocji nie mówcie innym rodzicom jaka liczba jest na waszej karteczce. Jeśli ktoś z was wydedukuje, że jego dziecko pali to niech rozpocznie rozmowę dyscyplinującą z dzieckiem i koniecznie napisze email do naszego informatyka. Informatyk umieści na naszej stronie internetowej komunikat informujący, ile dzieci w naszej klasie pali." Przez tydzień była cisza, nic w Internecie nie pojawiło się, dopiero po tygodniu co niektóry dzieciak dostał burę (a może i gorzej:-) a jak ustalono w niektórych domach był wrzask nie do opisania! Na początku słychać było jak gdyby "plask", "plask" i potem krzyk w niebogłosy "już nigdy!, już nigdy!". Powtarzało się to regularnie przez kilka kolejnych dni! Ile dzieciaków pali papierosy? Zadanie 37 Kiepski szpital↥
Do szpitalnej przychodni zgłasza się chory, cierpiący na wszelkie możliwe choroby zakaźne. Każde badanie wykonuje się tylko wówczas, gdy lekarz założy rękawiczkę. Czy pacjent może być zbadany przez tych trzech lekarzy, tak aby lekarze nie nabawili się dodatkowej choroby? Zadanie 38 Oskarżyciel↥
Pewien oskarżyciel, nie wiadomo czy kłamca czy prawdomówny, powiedział o Piotrze i Pawle: A co zrobić w sytuacji, gdy oskarżyciel mówi: Oskarżyciel mówi tak: Zadanie 39 Hotel↥Trzech podróżnych poszło do hotelu. Portier powiedział,że nocleg kosztuje po 100 zł od osoby czyli w sumie podróżni zapłacili 300 zł. Gdy kierownik hotelu sprawdzał rachunki stwierdził, że portier dał podróżnym jeden pokój trzyosobowy, który kosztuje 250 zł, kazał więc rano zwrócić 50 zł. Portier pomyślał oddam tylko 30 zł, bo 50 zł nie dzieli się przez 3, a różnicę wezmę sobie. Jak pomyślał tak zrobił. Policzmy: każdy z podróżnych zapłacił, po uwzględnieniu zwrotu, 90 zł czyli razem zapłacili 90·3=270 zł, portier "skubnął" 20 zł czyli razem jest 270 + 20 = 290 zł. A miało być 300 zł. Kto tu jeszcze zarobił "na lewo" 10 zł? Zadanie 310 Klepsydry↥
Zadanie 311 Wędrówka↥Ilu tragarzy powinien wynająć podróżny, który chce przejść przez pustynię. Droga przez pustynię trwa sześć dób. Każdy z tragarzy i sam podróżnik mogą unieść racje żywności i wody dla jednej osoby tylko na cztery doby wędrówki? Zadanie 312 Ryby↥ Sprawdź rozwiązanie
Później drugi rybak przebudził się, wyrzucił jedną rybę i wziął jedną trzecią pozostałych ryb. Ostatni też stwierdził, że po wyrzuceniu jednej ryby reszta dzieli się przez trzy. Wziął więc ⅓ pozostałych ryb. Jaka minimalna ilość ryb wchodzi w rachubę? Zadanie 313 Wstęga Mobiusa↥
(1) Co otrzymamy, jeśli przetniemy wstęgę po środku? (2) Co otrzymamy, jeśli będziemy ciąć wstęgę w odległości ⅓ szerokości od brzegu? (3) Pasek papieru skręcamy o 360o i sklejamy końce. Co otrzymamy jeśli przetniemy tę wstęgę po środku? Zadanie 314 Dętka↥Wyjmujemy z dętki wentyl, tak żeby powstał większy otwór. Przez ten otwór przeciągamy dętkę na drugą stronę. Co otrzymamy? Zadanie 315 Węzeł czterowymiarowy↥Człowiek nie może sobie wyobrazić przestrzeni czterowymiarowej ale, przy pewnym wysiłku, może zbadać własności takiej przestrzeni. Czy można zawiązać supełek na linie w czterech wymiarach? Zadanie 316 Łańcuch w czterech wymiarach↥Czy można zakuć kogoś łańcuchem w czterech wymiarach? Zadanie 317 Płaszczaki↥Aby "łatwiej" wyobrazić sobie zakrzywioną przestrzeń można badać powierzchnię kuli. Ĺťeby było jeszcze "łatwiej" umieszcza się na tej powierzchni dwuwymiarowe ludziki nazwane przez A. Einsteina płaszczakami. Płaszczak widzi, że jego powierzchnia jest rozległa i nie może zobaczyć wypukłości charakterystycznej dla kuli. Mądry płaszczak po pewnym czasie dochodzi do wniosku, że jednak powierzchnia kuli jest zakrzywiona lub całkiem nie podobna do płaszczyzny bo
Jak wygląda płaszczak? Jak się porusza? Jak się odżywia? Jak widzi? Jak wygląda jego domek? Jak widzą się nawzajem? Narysuj płaszczaka. Zadanie 318 Kostka czterowymiarowa↥
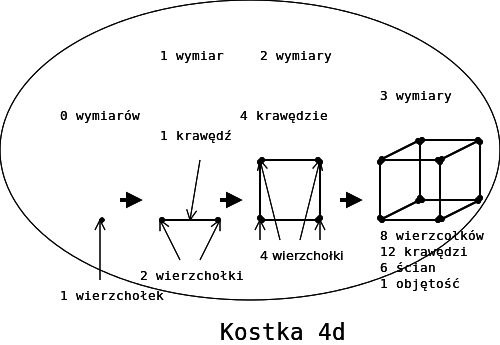
Rysunek przedstawia jak krok, po kroku można rysować kostkę czterowymiarową zaczynając od przestrzeni zerowymiarowej. Jak widać ilość wierzchołków podwaja się przy przejściu do przestrzeni o wyższej liczbie wymiarów.
Na powyższym rysunku pokazano przez analogię z niższymi wymiarami, jak skleić kostkę czterowymiarową z ośmiu sześciennych klocków. Jak widać trzeba będzie zginać kostki wzdłuż płaszczyzn! Najłatwiej jest zrobić kostkę dwuwymiarową: bierzemy cztery patyczki połączone zawiaskami, zginamy pod kątem prostym i potem sklejamy wolne końce. Tak samo robimy kostkę 4d. Sześciany łączymy zawiasami trójwymiarowymi, zginamy pod kątem prostym, kleimy pasujące ścianki i mamy kostkę!
Zadanie 319 Kula czterowymiarowa↥Czy kula czterowymiarowa ma powierzchnię? Zadanie 320 Mleczny paradoks↥Mleko zawiera 99% wody. Kupiłeś 1 litr mleka. Ile wody należy odparować aby pozostałe mleko zawierało 98% wody? Zadanie 321 Gdzie jest błąd?↥
Zadanie 322 Funty i pensy↥Jeden funt to 20 pensów. Jeden chleb kosztuje X funtów i Y pensów. Kilka chlebów kosztuje Y funtów i X pensów. Ile kosztuje chleb? |
Z powodu wielkich zaniedbań zabrakło rękawiczek ochronnych na zakaźnym oddziale pewnego szpitala. Zostały tylko dwie sztuki. W przychodni pracuje trzech lekarzy, niestety chorych na trzy różne choroby zakaźne - co też jest niewyobrażalnym zaniedbaniem.
Mam dwie klepsydry, w jednej piasek przesypuje się w ciągu 7 minut a w drugiej w ciągu 11 minut.
Jakie odstępy czasu mogę mierzyć tymi klepsydrami? Czy, na przykład, można odmierzyć 3 minuty?
Trzech rybaków wybrało się na połów. Po powrocie położyli się spać. Po pewnym czasie jeden z nich przebudził się, stwierdził, że ilość ryb nie dzieli się przez 3 ale gdy wyrzucił jedną z ryb to reszta podzieliła się przez 3, wziął więc jedną trzecią ryb i poszedł.
Wstęga Mobiusa jest to powierzchnia mająca tylko jedną stronę i jeden brzeg. Widać to dokładnie na rysunku. Wstęgę można wykonać z paska papieru, skręcenie go o 180o i sklejenie końców.
