| |
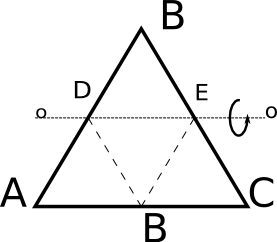
Nierówne jest równe!Narysujmy trójkąt i zegnijmy go wzdłuż przerywanej linii jak na rysunku. Jest oczywiste, że długość AD + DB + BE + EC jest taka sama jak AB + BC, to widać z rysunku. Taka równość jest prawdziwa dla każdego trójkąta, chyba nie trzeba tego udowadniać, jest to widoczne.
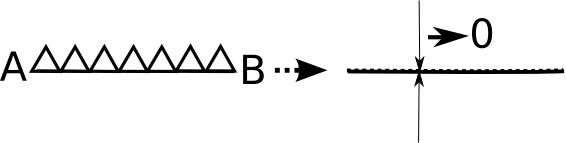
Powstają w ten sposób dwa mniejsze trójkąty, z każdym z nich robimy podobnie - zginamy w połowie. Czynność tę powtarzamy tak wiele razy aż łamana krzywa pokryje się z podstawą trójkąta AB.
Widać, że długość łamanej jest zawsze taka sama i równa długości AB + BC. Z drugiej strony jest jasne, że w końcu łamana pokryje się z podstawą i w takim razie musi być równa długości AC! AB + BC = AC!Z geometrii i z doswiadczenia wiemy, że zawsze suma długości dwóch boków w trójkącie jest większa od trzeciego boku! Chyba, że szkolna geometria nie jest prawdziwa! |