Dziwna krzywa.
Nieskończona ale krótka linia
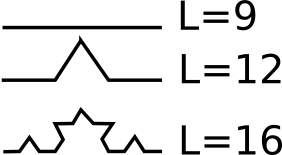
Rozumiecie cokolwiek z tego tytułu? Raczej wygląda to na bełkot! A czy zmienicie zdanie jak udowodnimy, że długość krzywej, dosyć łatwej do narysowania, jest nieskończenie wielka?
Zaczynamy od odcinka o długości dajmy na to 9 cm (żeby lepiej się dzieliło), dzielimy ją na trzy równe części, środkową część wyrzucamy, na środkowej części budujemy dwa boki trójkąta równobocznego. Długość otrzymanej krzywej będzie 12 cm.
Teraz będziemy powtarzać powyższą operację w kółko: każdy segment dzielimy na trzy, wyrzucamy część środkową a na środkowej części budujemy dwa boki trójkąta. teraz długość będzie 16 cm potem 16*(4/3) czyli 21,33..., w następnym kroku 21,33..*(4/3)=28,44.., potem 37,92.., 50,56.., 67,42..., aż otrzymamy taki obrazek (prawda, że śliczny):
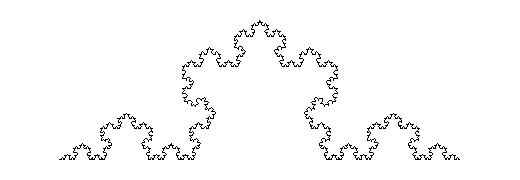
Widać, że długość rośnie w postępie geometrycznym. Wyrazy takiego ciągu albo maleją do zera (nie nasz przypadek) albo są stałe (nie nasz przypadek) albo rosną do dowolnie dużych liczb (dążą do nieskończoności) i z takim właśnie przypadkiem mamy tu do czynienia. Innej możliwości nie ma.
Jak widać na rysunku graniczna krzywa jest troszkę powyginana ale można rozpiąć na niej nitkę i przekonać się, że na pewno nie trzeba rozwinąć całej szpulki żeby ją zmierzyć! Długość jest raczej skończona, a z matematyki wychodzi inaczej! Po drugie, skoro możemy ją narysować, to nie może być długość tej krzywej nieskończona bo skąd wziąć tyle atramentu? Coś nie tak jest z tą matematyką i rozbieżnością postępu geometrycznego.

