| |||||||||
Rozwiązywanie zadań z fizykiSeweryn WegielnikZadanie o toczącej się kuliTocząca się kulaPo poziomej powierzchni toczy się, bez poślizgu, kula. Prostopadle do toru ruchu kuli ustawiono ściankę. Oblicz końcową prędkość kuli po odbiciu od ścianki. Prędkość początkowa kuli wynosi 36 km/godz. Analiza zadania↥
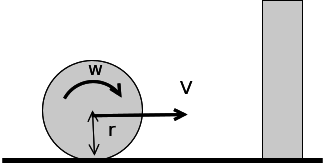
Pierwszym etapem do rozwiązania zadania jest jego zrozumienie. Dobrze jest w tym celu wykonać rysunek (rysunek 1).
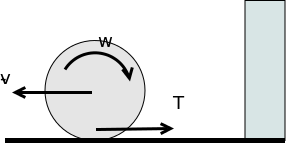
Po odbiciu od ścianki zmieni się kierunek prędkości na przeciwny. Kierunek wirowania nie zmieni się. Dzięki temu pojawi się siła tarcia, która spowoduje spowalnianie ruchu postępowego kuli i zmianę ruchu obrotowego kuli. W końcu, kula będzie wirować tak, że nie wystąpi poślizg.Po odbiciu sytuacja będzie jak na rysunku 2. Założenia↥Raczej zawsze, podczas rozwiązywania problemów fizycznych, musimy zrobić pewne uproszczenia, idealizacje, założenia upraszczające:
Rozwiązanie↥W zadaniu mamy następujące zjawiska fizyczne:
Rozwiązanie
Toczące się bez poślizgu kula odbija się od pionowej ściany. Oblicz prędkość obrotową kuli po odbiciu. Rozwiązanie
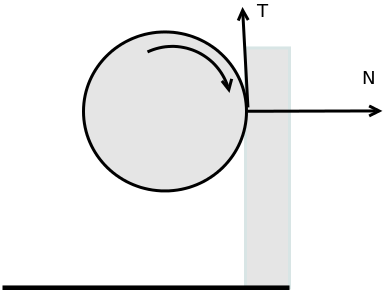
Punkt styczności powierzchni kuli w momencie uderzenia o ścianę ma prędkość skierowaną do dołu (patrz rysunek 3) w związku z tym pojawia się siła tarcia T, skierowana do góry. Niech średnia siła nacisku kuli na ścianę wynosi N. Niech czas zderzenia wynosi τ Obliczmy siłę tarcia: T = N · k .....I, moment tej siły spowoduje zmniejszenie prędkości wirowania kuli. Wykorzystamy zależność zmiany momentu pędu kuli od czasu działania momentu siły Mf: Wychodzimy od analogu II Zasady dynamiki dla ruchu obrotowego: Mf = I · ε = I · Δω/τ .....II Mnożąc przez τ mamy: Mf·τ=I · Δω .....III Za moment siły wstawiamy obliczone wartości: Mf=T · r = N · k · r..... IV ale przy zderzeniu sprężystym kuli ze ścianą następuje zmiana pędu kuli równa: 2 · m · Vo (przed zderzeniem pęd był ppoczątkowy=p a po zderzeniu pkońcowy=-p, stąd różnica pędu: Δp=ppoczątkowy-pkońcowy=p-(-p)=2·p). Ponieważ ta zmiana pędu nastąpiła w czasie τ więc możemy obliczyć średnią siłę nacisku: N = 2 · m · Vo/τ.... V Zaraz kończymy - cierpliwości! Wstawiamy V i IV do II i obliczamy zmianę prędkości kątowej: Δω=5·k·Vo/r = 5·k·ωo;. Kula po odbiciu od ściany zmniejsza swoją prędkość wirowania o wartość 5·k·ω. Uff! DyskusjaW przypadku dużego tarcia kula może przestać wirować.
Δp|/τ=2·m ·V Stąd v| = 2·Vo·k. Kula zawsze podskoczy przy ściance!
Jest to niezmiernie ciekawe!
Rower jedzie z prędkością 18 km/godz. Średnica koła wynosi 60 cm. Jaka jest prędkość kątowa koła? Ile wynosi największa prędkość w rowerze? Jaki punkt porusza się najszybciej? Ile obrotów na sekundę wykonuje koło?
Łyżwiarz wykonuje piruet z rozpostartymi rękoma. Wykonuje 2 obroty/sek. Jeśli po ściągnięciu ramion moment bezwładności zmniejszył się dwukrotnie to ile razy zmieni się jego energia kinetyczna? Jaka siła wykonała pracę potrzebną do zmiany energii?
Cegła porusza się po doskonale gładkim podłożu skośnie do ściany. Cegła jest równoległa do ściany. Kąt padania wynosi α. Pod jakim kątem cegła odbije się od ściany, jeśli współczynnik tarcia cegły o ścianę wynosi f.
W sporcie: piłce nożnej, siatkówce itp znane jest pojęcie "podkręconej" piłki. Polega to na tym, że piłka nie porusza się po prostej a zakrzywia w dziwny sposób swój tor. Jakie zjawiska są za to odpowiedzialne?
Oblicz kąt odbicia toczącej się bez poślizgu kuli od ściany. Czy ten kąt jest większy od kąta padania?
Cienkościenna rura toczy się bez poślizgu i odbija się od prostopadle ustawionej ścianki. Zaniedbując tarcie pomiędzy powierzchnią rury a ścianką oblicz końcową prędkość rury.
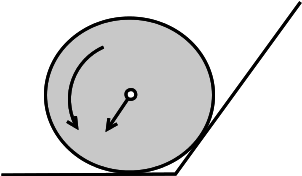
Przeanalizuj staczanie się kuli ze skośnej deski (kąt nachylenia β).
Niech współczynnik tarcia kuli o deskę i podstawę wynosi k.
Jaki jest maksymalny kąt nachylenia deski, przy którym jeszcze nie występuje poślizg? Zbadaj co się dzieje, gdy kula zderza się z poziomą podstawą.
Czy kula odskaczy pod takim samym kątem pod jakim uderzyła o deskę? Czy prędkość kuli w czasie poruszania się po podłożu będzie taka jak w momencie zetknięcia z podłożem?
|