 | ||||||||||||||||||||||||||||||||||||||||||||||
Podstawy FizykiSeweryn Wegielnik
Przestrzeń i czasPodstawowe pojęciaPewnik podstawowa prawda w matematyce. Zasada podstawowa prawda w fizyce i naukach przyrodniczych. Dogmat podstawowa prawda w religii i naukach humanistycznych np. kanon w sztuce. Pewnik, zasada... to prawdy nie dające się w żaden sposób udowodnić, są tak oczywiste, że nawet najgorszy niedowiarek musi przyznać, że tak jest. Należy przyjąć je na wiarę. Każda próba dowodu kończy się poważnymi problemami. Na przykład jeden z pewników Euklidesa (piąty) mówi, że przez punkt poza daną prostą można poprowadzić tylko jedną prostą równoległą do danej prostej. Jest to, na pierwszy rzut oka, oczywiste ale wygląda jak twierdzenie więc przez tysiące lat matematycy starali się udowodnić ten pewnik - zawsze z niepowodzeniem! Dopiero zmiana tego pewnika, na jak gdyby absurdalny, że można poprowadzić dowolną (łącznie z zerową) ilość prostych równoległych dała podwaliny pod nowe badania przestrzeni, tzw przestrzeni nieeuklidesowych. Badanie podstawowych zasad prowadzi często do nowych pomysłów i lepszych zasad. Prawo (odpowiednik twierdzenia w matematyce): zaobserwowana prawidłowość, przeważnie dająca się wytłumaczyć w oparciu o zasady. Nie zawsze jest to proste. Doświadczenie: podstawa fizyki. Wyniki eksperymentu fizycznego są potwierdzane przez niezależne zespoły badawcze. Często doświadczenie prowadzi do lepszego zrozumienia zasad lub stworzenie podstaw do zmiany obowiązujących zasad. Każde doświadczenie musi być przeprowadzane wiele razy i za każdym razem prowadzić do takich samych wyników. Doświadczenie może dać wynik sprzeczny z obowiązującymi zasadami, na co tylko czekają fizycy teoretycy, co pozwala na zrewidowanie podstaw. Często przeprowadza się doświadczenia w oparciu o wyniki teoretycznych badań. Wyniki takich badań są kluczowe dla zrozumienia podstaw fizyki. Pięknym przykładem są teoretyczne przesłanki zrobione przez Mendelejewa. Tworząc Układ Okresowy Pierwiastków Mendelejew przewidział, że w przyrodzie muszą znajdować się pierwiastki, których właściwości przewidział nazwał je eka-bor, eka-glin i eka-krzem. Przewidział on właściwości tych pierwiastków na podstawie ich położenia w układzie. Potwierdzeniem słuszności jego przypuszczeń było odkrycie w roku 1875 nowego pierwiastka - galu, którego właściwości odpowiadały przewidzianym przez Mendelejewa dla eka-glinu. Kolejne odkrycie pierwiastka skandu w roku 1879 stanowiło kolejne potwierdzenie słuszności Mendelejewa. Skand był jego eka-borem. Ostatni z te triady eka-krzem został odkryty w 1886 roku i nazwany germanem. Negatywny wynik doświadczenia zawsze zaprzecza teorii, która zasugerowała inny wynik. Doświadczenie może nie dać wyniku potwierdzającego co nie przeczy teorii. Na przykład fizycy teoretycy przewidują istnienie monopolu - cząstki magnetyzmu podobnie jak w elektryczności ładunku elektrycznego. Mimo wielu badań nie wykryto takiej cząstki. Nie oznacza to, że teoria jest zła. PrzestrzeńPrzestrzeń nasza jest z bardzo dobrym przybliżeniem euklidesowa. Co to oznacza? Wszystkie doświadczenia udowadniają nam, że przykładowo: suma kątów w trójkącie daje w sumie dwa kąty proste czyli 180o lub jak kto woli π radianów albo 200 gradów albo 18 rumbów itp; zachodzi również ciekawa zależność w trójkącie o bokach a = 3, b = 4, c = 5 a mianowicie:a2 + b2 = c2Zależność ta znana jest od najdawniejszych czasów. Najciekawsze jest to, że kąt pomiędzy a i b jest prosty równy ½π radianów.
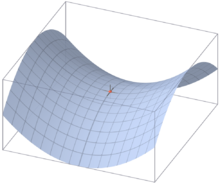
Już starożytni Egipcjanie stosowali ten fakt przy wyznaczaniu kątów prostych a obecnie drwale stosują trójkąt o takich bokach, zbity z desek, do równego budowania pryzm z bali. Jak się okazuje każde twierdzenie wynikające z Pewników Euklidesa jest prawdziwe. Wszelkie doświadczenia potwierdzają euklidesowość naszej Przestrzeni. Zachodzi pytanie: A czy mogłoby być inaczej? Czy istnieje taka przestrzeń, w której nie obowiązują pewniki Euklidesa? A może nasza przestrzeń, gdyby zrobić dokładniejsze pomiary, odbiega nieco od tej ślicznej naszej koncepcji? Przykładem przestrzeni nieeuklidesowej może być powierzchnia kuli. Łatwo przekonać się, rysując na globusie trójkąty, że suma kątów w trójkącie jest większa od ½π. Na przykład rysując dwa południki aż do przecięcia z równikiem widać, że powstały trójkąt jest podwójnie prostokątny! ma dwa kąty proste w wierzchołkach na równiku i w takim razie suma kątów w trójkącie na globusie jest zawsze większa od ½π. Widać, że aby określić, czy przestrzeń czasami nie jest "krzywa" wystarczy zbadać sumę kątów trójkąta nie trzeba patrzeć na przestrzeń z innego wymiaru. Gdyby nasza przestrzeń była zakrzywiona to w żaden sposób nie odczulibyśmy tego - powyginałoby nas ale tego nie widzielibyśmy. Dopiero rysując, raczej duży, żeby zaobserwować efekt, trójkąt moglibyśmy wędrować od wierzchołka do wierzchołka z kątomierzem i mierzyć kąty. Może suma nie byłaby ½π? Skoro powierzchnia nie jest płaska to moglibyśmy wprowadzić krzywiznę ρ jako liczbową miarę zakrzywienia. W przypadku kuli przyjmuje się odwrotność promienia kuli: ρ = 1 / RDokładniej: dla każdej powierzchni możemy narysować dwa koła styczne do powierzchni wzajemnie prostopadłe. Oznaczając r1 i r2 jako promienie tych kół można określić krzywiznę wzorem: ρ = 1 / √ r1·r2W przypadku przestrzenie trójwymiarowej trudniej jest wyobrazić sobie krzywizną takiej przestrzeni ale można przyjąć, że dla każdego trójkąta prostokątnego o przyprostokątnych a i b oraz przeciwprostokątnej c, mogą zachodzić trzy przypadki:
Wymiar przestrzeniWszystkie ciała w naszej przestrzeni są trójwymiarowe: każde ciało posiada długość, szerokość i wysokość. Mówimy, że Nasza Przestrzeń jest trójwymiarowa. Żadne doświadczenie nie przemawia za istnieniem jakiegoś dodatkowego wymiaru przestrzennego. Nie doświadczamy w żaden sposób czwartego wymiaru. Moglibyśmy jednak opisać na przykład kostkę czterowymiarową:
W tabelce tej łatwo wykryć pewne prawidłowości i z tych prawidłowości wynika "kształt" kostki. Jest tam kilka objętości oraz dodatkowo czterowymiarowy odpowiednik objętości, który nazwaliśmy hiper objętością. Czyli kostka o krawędzi 1 m ma objętość 8 m3! Co to jest hiper objętość - nie wiemy bo nie znamy obiektów czterowymiarowych! Jak widzimy ludzik "czterowymiarowy" jest niemożliwy do wyobrażenia a ludzik "dwuwymiarowy" (2ludzik) myślicie, że łatwo narysować taki stwór - spróbujcie! Chodzić przebierając nogami jak my nie może! Musi skakać! Może patrzeć się tylko w jedną stronę! Dziwak jakiś!
Zadania
CzasIstnienie czasu jest dla nas oczywiste. Własności czasu są proste: Czas równomiernie "płynie", jest jednokierunkowy i jest wieczny. Wierzymy, że za tysiące lat czas będzie tak samo płynął. Przez tysiąclecia uczeni i myśliciele nie zawracali sobie głowy czasem. Do mierzenia czasu używa się zegarów. W zegarze jest zawsze jakieś urządzenie, którego stan powtarza się periodycznie. Może to być wahadło, drgający kryształ kwarcu itp. Uważamy, że jeśli zegar "chodzi" to będzie tak chodziła zawsze, nie ma tu znaczenia czy się spieszy czy późni. W przypadku niedokładności możemy zawsze obliczyć odpowiednie poprawki. Czas jest absolutny. Do początku Dynamika KlasycznaPodstawowe pojęcia
Do początku Teoria grawitacji powszechnej
W trakcie tworzenia
Do początku Szczególna Teoria Względności
W trakcie tworzenia
W trakcie tworzenia
Do początku Ogólna Teoria Względności
W trakcie tworzenia
Do początku Elektryczność i magnetyzmPodstawowe pojęcia
Czym jest prąd elektryczny?Jak podano w "Podstawowych pojęciach" nie można odpowiedzieć na pytanie zadane w tytule ale można podeprzeć się przykładami, które pomogą naszej wyobraźni. Chyba najlepszym przykładem jest porównanie prądu do jakiegoś wiru np. wiru w wodzie, tornada itp. Jeśli przypatrzymy się wirowi wody podczas spuszczania wody w wannie to zauważymy centrum w postaci linii krzywej - woda tam porusza się bardzo szybko a w samym centrum tworzy się lej. Można powiedzieć, że to centrum jest jakąś osobliwością. Wokół tej krzywej wiruje woda. Im dalej od centrum tym prędkość jest mniejsza.Powinniśmy zbadać prędkość wody w zależności od centrum. Wtym celu można na wodę rozsypać trochę mąki, zmielonego pieprzu i zmierzyć prędkość (np. wykonując dwie fotografie w krótkim odstępie czasu). Obserwują wiry na wodzie można spostrzec, że dwa wiry kręcące się zgodnie jak gdyby przyciągają się a kręcące się przeciwnie odpychają się.
Zadania
Do początku Optyka
W trakcie tworzenia
Do początku Termodynamika
W trakcie tworzenia
Do początku Fizyka atomowa
W trakcie tworzenia
Do początku Fizyka jądrowa
W trakcie tworzenia
Do początku Cząstki elementarne
W trakcie tworzenia
Do początku Rozstrzygające doświadczenia
W trakcie tworzenia
Do początku Podstawowe równania fizyki
W trakcie tworzenia
Do początku Liczby, które rządzą Światem
W trakcie tworzenia
Do początku MatematykaUkład współrzędnychPowrot do dynamikiDo określenia położenia jakiegokolwiek punktu wygodnie jest zbudować układ współrzędnych. Ponieważ w naszej |
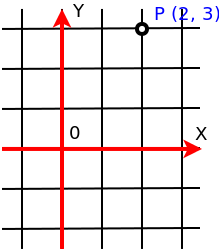przestrzeni możliwe jest określenie odległości pomiędzy dwoma punktami przy pomocy liniału, więc możemy pokryć całą przestrzeń przy pomocy kratownicy. Jeśli decydujemy się na dokładność 1 m, kratownica może wyglądać tak jak na rysunku.